Audio: frequency modulation (0:06)
frequency modulation plays two sounds demonstrating simple Frequency Modulation (FM). The first sound is created by frequency modulating a 440Hz carrier with a 1,613Hz modulator using a variable modulation index rising from 0 to 4. A synthetic bell, the second sound, is created by frequency modulating a 400Hz carrier with a 560Hz modulator using a variable modulation index rising from 0 to 10. The frequency modulation figure shows the spectrograms of the two sounds side by side.
Frequency Modulation (FM) uses a modulator to change the frequency of a carrier.
FM synthesis is the use of FM in music. The technique was pioneered by the composer John Chowning in 1967 and incorporated into commercial hard synths from the 1970s onwards.
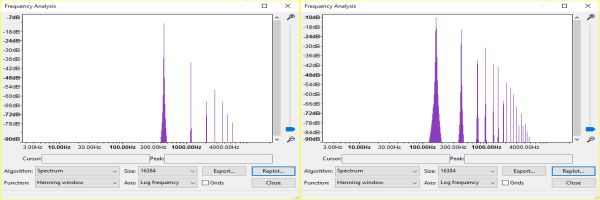
FM is timbrally much richer than Ring Modulation or Amplitude Modulation. Both RM and AM produce only first-order sidebands, whereas FM produces multiple-order sidebands. The frequency of the sidebands in FM is determined by the relationship between the carrier frequency and the modulator frequency, just as it is in RM and AM. The difference is that FM produces not just first-order sidebands, c+m and c-m, where c is the carrier frequency and m is the modulator frequency, but also second-order sidebands, c+2m and c-2m, third-order sidebands, c+3m and c-3m, and so on.
One of the most important factors in FM is the frequency modulation index, or FM index. It determines the amplitude of the modulator, which, in turn, determines the number of sidebands that are produced and their amplitude.
The FM index is the ratio of the carrier frequency to the modulating frequency. An index of zero results in no FM, all that is heard is the carrier. An index of 1 will drive the carrier frequency upward and downward by 440Hz if the modulating frequency is 440Hz, an index of 2 by 880Hz and so on. As the modulation index rises, more sidebands become audible, and the timbre of the output becomes denser, because the number of frequencies increases. The sound becomes brighter too, because more of the frequencies are higher frequencies.
The value of the FM index determines the amount by which the carrier frequency varies. Unlike the AM index, which is always limited to a maximum of one to avoid distortion, the FM index can exceed one and values of 4 or 5 or higher are not uncommon. The only constraint is that the value of the FM index should not lead to aliasing.
In frequency modulation the modulation index of the first sound is 4. This drives the frequency of the 440Hz carrier up and down by 1760Hz, noting that negative frequencies wrap around to their positive values. In the second sound the modulation index is even higher, 10. It drives the frequency of the 400Hz carrier up and down by 4,000Hz.
The modulation index also determines the amplitude of the modulator, which, in turn, determines the number of sidebands that are produced and their amplitude. It might seem strange that frequency modulation affects amplitude but this is indeed the case. Trying to calculate the frequency and amplitude of sidebands in FM is much more difficult than it is in RM and AM and requires a knowledge of seriously advanced maths, Fourier Analysis and Bessel functions in particular. In simple terms, the higher the index, the more sidebands there are, the richer the timbre.
Simple FM is a powerful synthesis technique. It is quite amazing that two humble sine waves can produce an FM output that is harmonically rich. The impact of FM is much more pronounced than that of RM or AM because of the impact of multiple sidebands. FM is an extremely useful technique for writing complex sound effects and for writing instantaneous harmony.